Andres F. Galvis
School of Mechanical Engineering and Center for Computing in Engineering & Sciences – University of Campinas
Metallic materials have been widely studied due to its important role in various industry fields, that is the reason why researches have been focused their efforts to understand an initial question: how do these materials fail? In the beginning, failure theories such as damage or fracture mechanics were proposed, using mathematical approaches supported by experimental observations. These approaches allowed to predict the catastrophic failure of mechanical elements under severe environmental conditions. Otherwise, the mentioned ways to quantify the material weakening were not enough, because many physical effects were not contemplated. In fact, the limitation was clearly caused by the lack of validation procedures of more sophisticated theories.
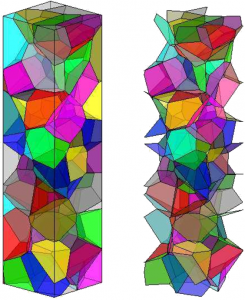
Metals at the microscale: polycrystalline structure and interfaces
New industrial developments and the emerging of advance fields such as applications of nanotechnology, gave us a response to justify why is necessary to improve the confidence of failure theories. Hence, the birth of another type of analysis appeared the well-known Multiscale approaches. Imagine that, if in the past basic methods were successful with lack of physical considerations, now more realistic effects could be taken into account in the same problem owing to the inclusion of a new small scale (the proper microstructure material) in specific points where the mechanical element could fail.
Why this level of detail is important? It helps us to better understand how the failure phenomenon works in these materials. A simple and logic concept we can cite here is while the scale is reduced, the material configuration becomes more chaotic being very difficult to get its computational model. For clarifying the concept, consider a determined mechanical element that should accomplish some task. Critical points will appear at several stages, with multiscale modeling, we could analyze each of them internally to accurately discover the real caused of failure. This procedure could lead us to an element optimization an optimization according to its function.
Researches from the CCES have been looking for the development of a multiscale models to treat failure from macro to nanoscale level. As indicated in the figure, the micro and nano models provide relevant information in terms of behavior and possible failure zones. In this type of approaches, we need to select adequate numerical methods for reproducing the materials artificially. Taking into account the extensive experience of the research group of Prof. Paulo Sollero on modeling heterogeneous materials, a new multiscale framework was proposed using by the first time the boundary element method and molecular dynamics together.
Both numerical methods get to model properly the three scales. Molecular dynamics provides enough critical data to quantify failure at the nanoscale, which is directly applied on the microscale. By doing so, the crack propagation between grains onsets, producing a weakening on the macroscale. It can be perceived the increase in the level of detail, mainly in the atomistic construction of the interfaces. The final results were partially published on international journals and presented in a Ph.D. thesis.
The research group of Prof. Paulo Sollero at the School of Mechanical Engineering – Unicamp, simulates failure conditions using the boundary element method on polycrystalline, composites and bone structures applying several approaches such as molecular dynamics or quasi-continuum methods, according to the physical problem. All these analyses are possible employing high-performance computational implementations.
Associated scientific papers:
Andres F. Galvis. Multiscale Modeling of Dynamic Failure in 3D Polycrystalline Materials using BEM and MD, Ph.D. thesis, School of Mechanical Engineering, University of Campinas (2019).
Andres F. Galvis., Rene Q. Rodríguez., Paulo Sollero. Dynamic analysis of three-dimensional polycrystalline materials using BEM. Computers & Structures 200, pp. 11-20, 2018.
Andres F. Galvis., Rene Q. Rodríguez., Paulo Sollero. Analysis of three-dimensional hexagonal and cubic polycrystals using the boundary element method. Mechanics of Materials 117, pp. 58-72, 2018.
Alvarez, J.E., Galvis, A.F., Sollero, P. Multiscale dynamic transition of 2D metallic materials using the boundary element method. Computational Meterials Science 155, pp. 383-392, 2018.
Rodríguez, R.Q., Galvis, A.F., Sollero, P., Tan, C.L. and Albuquerque, E.L. Transient dynamic analysis of generally anisotropic materials using the boundary element method. Acta Mechanica 229(4), pp. 1893–1910, 2018.
Galvis, A.F., Sollero, P. 2D Analysis of Intergranular Dynamic Crack Propagation in Polycrystalline Materials a Multiscale Cohesive Zone Model and Dual Reciprocity Boundary Elements. Computers & Structures 164, pp. 1-14, 2016.

