Andres F. Galvis
Faculdade de Engenharia Mecânica e Centro de Computação em Engenharia e Ciências – Universidade de Campinas
Os materiais metálicos têm sido amplamente estudados devido ao seu importante papel em vários campos da indústria. Por esta razão, as pesquisas têm concentrado seus esforços em entender uma questão inicial: como estes materiais falham? No começo, as teorias de falha, como dano ou mecânica de fratura, foram propostas utilizando abordagens matemáticas suportadas por observações experimentais. Estas abordagens permitiam prever a falha de elementos mecânicos sob determinadas condições de utilização. Porém, estas teorias não eram suficientes para quantificar o enfraquecimento dos componentes, já que muitos efeitos físicos não eram analisados. Portanto, a limitação era claramente causada pela falta de procedimentos de validação mais sofisticadas.
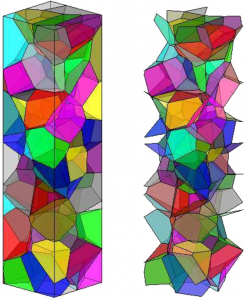
Metais em microescala: estrutura policristalina e suas interfaces
Os novos avanços industriais e o surgimento de campos de estudo mais complexos, como a nanotecnologia, nos deram uma resposta para justificar o motivo pelo qual é necessário melhorar a confiança das teorias de falha. Tais avanços possibilitaram o nascimento da análise conhecida como multiescala. Imagine que, se no passado métodos básicos foram bem-sucedidos com a falta de algumas considerações físicas, agora efeitos mais realistas poderiam ser considerados no mesmo problema devido à inclusão de uma nova pequena escala (a própria microestrutura do material) em pontos específicos onde o elemento mecânico pode falhar.
Por que esse nível de detalhe é importante? Isso nos ajuda a entender melhor como o fenômeno da falha ocorre nestes materiais. Um conceito simples e lógico que podemos citar aqui é: enquanto a escala é reduzida, a configuração do material torna-se mais caótica, sendo muito difícil aplicá-la em um modelo computacional. Para esclarecer este conceito, considere um determinado elemento mecânico que deve realizar alguma tarefa, pontos críticos aparecerão em vários estágios e, com modelagem multiescala, poderíamos analisar cada um deles internamente para descobrir com precisão a real causa da falha. Este procedimento poderia nos levar a uma otimização do elemento de acordo com sua funcão.
Os pesquisadores do CCES têm buscando o desenvolvimento de um modelo multiescala para tratar falhas em diferentes níveis, desde a macro até nanoescala. Como ilustrado na figura, os modelos da micro e nanoescalas fornecem informações relevantes em termos de comportamento e possíveis regiões de falha. Neste tipo de abordagem, precisa-se selecionar métodos numéricos adequados para reproduzir artificialmente os materiais. Levando em conta a extensa experiência do grupo de pesquisa do Prof. Paulo Sollero na modelagem materiais heterogêneos, uma nova estrutura multiescala foi proposta utilizando, pela primeira vez, associação entre o método dos elementos de contorno e dinâmica molecular.
Juntos, os dois métodos numéricos conseguem modelar apropriadamente as três escalas. A dinâmica molecular fornece dados para quantificar a falha na nanoescala, que é aplicada diretamente microescala. Assim, a propagação da falha entre os grãos se dá produzindo um enfraquecimento na macroescala. Pode-se perceber o aumento no nível de detalhamento, principalmente na construção das interfaces. Os resultados finais foram parcialmente publicados em revistas internacionais e apresentados em uma tese de doutorado.
O grupo de pesquisa do Prof. Paulo Sollero na Faculdade de Engenharia Mecânica – Unicamp, simula condições de falha usando o método de elementos de contorno em policristalinos, compósitos e estruturas ósseas aplicando várias abordagens, como dinâmica molecular ou métodos quase-contínuos, de acordo com o problema físico. Essas análises são possíveis empregando ferramentas computacionais de alto desempenho.
Artigos científicos:
Andres F. Galvis. Multiscale Modeling of Dynamic Failure in 3D Polycrystalline Materials using BEM and MD, Ph.D. thesis, School of Mechanical Engineering, University of Campinas (2019).
Andres F. Galvis., Rene Q. Rodríguez., Paulo Sollero. Dynamic analysis of three-dimensional polycrystalline materials using BEM. Computers & Structures 200, pp. 11-20, 2018.
Andres F. Galvis., Rene Q. Rodríguez., Paulo Sollero. Analysis of three-dimensional hexagonal and cubic polycrystals using the boundary element method. Mechanics of Materials 117, pp. 58-72, 2018.
Alvarez, J.E., Galvis, A.F., Sollero, P. Multiscale dynamic transition of 2D metallic materials using the boundary element method. Computational Meterials Science 155, pp. 383-392, 2018.
Rodríguez, R.Q., Galvis, A.F., Sollero, P., Tan, C.L. and Albuquerque, E.L. Transient dynamic analysis of generally anisotropic materials using the boundary element method. Acta Mechanica 229(4), pp. 1893–1910, 2018.
Galvis, A.F., Sollero, P. 2D Analysis of Intergranular Dynamic Crack Propagation in Polycrystalline Materials a Multiscale Cohesive Zone Model and Dual Reciprocity Boundary Elements. Computers & Structures 164, pp. 1-14, 2016.

