Date: Feb 24, 2023.
Candidate: Guilherme de Souza Tavares de Morais
Advisor:
Prof. Dr. Rogerio Custodio
Abstract:
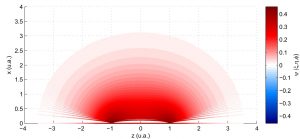
An alternative for solving the Schrödinger equation, the variational fixed-grid method, was developed. This method combines numerical differentiation, numerical integration and Gram-Schmidt orthonormalization techniques to calculate ground and excited states of quantum systems. It is a numerical method that does not use base functions, like conventional methods. Its development focused on the hydrogen atom and the molecular hydrogen ion in different curvilinear coordinate systems, admitting the free and confined system. This methodology depends on well-defined boundary conditions in all coordinates of the system. However, in some coordinate systems, there are no explicit boundary conditions at the points where the Jacobian of the coordinate system vanishes. An alternative based on transforming variables was suggested to overcome this difficulty, allowing boundary conditions to be created and allowing all points of the wave function to be optimized using the variational principle. With this transformation, the variational fixed grid method was extended to curvilinear coordinate systems that do not have well-defined boundary conditions, making it attractive to numerically solve different physical problems