This work presents the analysis of three-dimensional polycrystals in the microscale with different latticestructures, hexagonal closed package (HCP) and face centered cubic (FCC). In these materials, the grainedmedium is considered as a continuum elastic body. An artificial polycrystalline structure is modeled using theVoronoi tessellation to generate random morphological microstructures. To reproduce the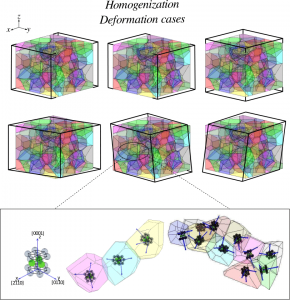 
stochastic effects,arbitrary crystalline orientations are distributed over the structure. The boundary element method (BEM) is usedto obtain the static displacement and tractionfields, with a fundamental solution for 3D general anisotropicmaterials based on double Fourier’s series. The macroscopic effective elastic properties are evaluated using theaverage homogenization technique and compared to the reference values through convergence statistical ana-lysis. Explicit schemes are presented in order to improve the computational load and decrease the time requiredby the main BEM application implemented on distributed memory architectures. Numerical examples are pre-sented showing the convergence of the results and comparisons of anisotropy level between these FCC and HCPmaterials using a recently proposed anisotropy factor.
Andres F. Galvis., Rene Q. Rodríguez., Paulo Sollero. Analysis of three-dimensional hexag- onal and cubic polycrystals using the boundary element method. Mechanics of Materials 117, pp. 58-72, 2018.