Nonlinear dynamic models for deep water subsea lifting operations.

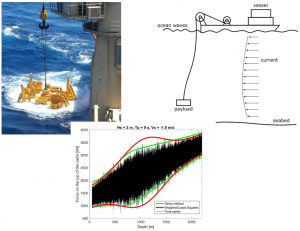
This thesis presents new models for the analysis of the nonlinear dynamics of subsea lifting operations. Focus in given on the development of new models and their implications on the planning and analysing of deep water subsea lifting operations. Among the points addressed in the thesis, the most relevant are the modelling of variable length cables, the statistical analysis of non-stationary time series, the dynamics of the system in super-harmonic resonances and the modelling of amplitude-dependent hydrodynamic coefficients. It is found that the lowering or lifting velocity has a direct impact on the static and dynamic forces acting on the system and also on the time of exposure of the system to random wave conditions. The selection of a suit-able velocity for the winch might be therefore used to optimize the operation. Two methods are also presented for the prediction of the design loads on the system when the system is modelled assuming a variable length cable. One of these methods, enables an accurate representation of the statistics of the response via a reduced number of independent random simulations in com-parison to traditional methods in the literature. Furthermore, semi-analytical solutions are pre-sented to analyse the dynamics of the system in super-harmonic resonance and when the hydrodynamic coefficients are amplitude-dependent. The procedure is considered accurate in comparison to time domain integration, but significantly faster. It is shown the impacts that super-harmonic resonances can have on the dynamics of the system, as in some scenarios the zones where these resonances occur might be the limiting design case in real operations. Finally, the use of amplitude-dependent hydrodynamic coefficients is found to be key for the analysis of deep water operations, as this formulation predicts variations in the extreme loads and on the depths where they occur, due to the variation of the natural frequency and damping of the system.