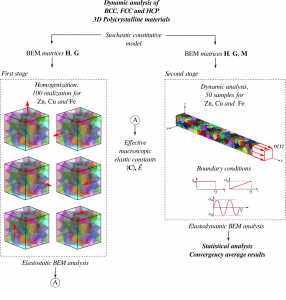
A new computational framework to analyse the microscale dynamic behaviour of three-dimensionalpolycrystalline materials with different lattice structures is presented. The absence of analytical solutionsfor these stochastic materials has been a challenge in validating the numerical results. In macroscaleanalysis, when the number of crystal aggregates in the microscale is large, polycrystalline aggregatesexhibit an effective isotropic nature. To model the elastodynamic effects, random crystalline orientationsand morphology configurations are used for each polycrystalline aggregate. The recently proposed funda-mental solution based on double Fourier series for general anisotropy coupled to the dual-reciprocityboundary element method is used. A drastic reduction in the degrees of freedom is achieved owing tothe nature of the boundary mesh. The stochastic time-dependent displacement wave under variousboundary conditions is evaluated, and the validation is carried out using homogenisation over the grainsurfaces. An assessment of the effective macroscopic properties of the available analytical isotropic mod-els is proposed, wherein the convergence is evaluated using statistical samples. Numerical results arepresented using a large number of simulations to obtain a good confidence interval.